The Theory Of Displacement

Introduction:

The moving of something from its place or position is called displacement. When any force applied to any object, the object starts to move. I have invented a formula to determine the value of displacement. 

Abstract:

The moving of something from its place or position is called displacement. Here we will discuss about the relationship between object’s momentum, mass, applied force and displacement. 

Method:

I have used this method for this formula. 

We know that- v²=u²+2as

                     Or, v²= 2as          [u=0]

                     Or, 2as= v²          [Transforms]

                     Or, as= v²÷2.       [Transforms]

                    So, as= v²÷2__________(i)

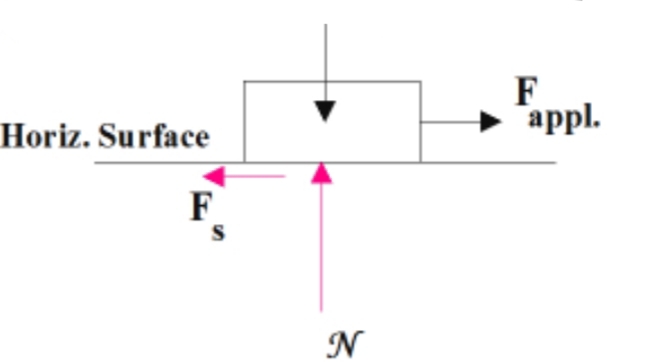
                        W= Fs

                           = mas.        [F= ma]

                           = m×(v²÷2)

                           = ½mv²

                           = m²v²÷2m [Multiplied by m÷m]

                           = p²÷2m.       [p=mv]

So, W= p²÷2m_____________(ii)

Conditionally, Fs= p²÷2m

                 Or, s= p²÷2Fm.   [Transforms]

So, s= p²÷2Fm____________(iii)

If p= 2p then- 

s'= (2p)²÷2Fm

  = 4p²÷2Fm

  = 4×(p²÷2Fm)

  = 4s

s'= 4s

If p= ½p then- 

s'= (½p)²÷2Fm

  = ¼p²÷2Fm

  = p²÷8Fm

  = ¼×(p²÷2Fm)

  = ¼s

So, s'=¼s

If the square value of object’s momentum increases, then the value of object’s displacement increases proportionally. If the square value of object’s momentum increases, then the value of object’s displacement increases proportionally. 

So, s∞ p²__________(iv)

If Fm= 2Fm then-

s'= p²÷2(2Fm)

   = p²÷4Fm

   = ½×(p²÷2Fm)

   = ½s

So, s'= ½s

If Fm= ½Fm then-

s'= p²÷2(½Fm)

   = 2p²÷2Fm

   = 2×(p²÷2Fm)

   = 2s

So, s'= 2s

If the value of applied force and mass increases, then the value of object’s displacement decreases disproportionally. If the value of applied force and mass decreases, then the value of object’s displacement increases disproportionally.

So, s∞ 1÷2Fm__________(v)

The graph of iv number equation- 

The graph of v number equation- 

From iv and v number equation, we get- 

s∞ p²__________(iv)

s∞ 1÷Fm__________(v)

So, s∞ p²×1÷Fm

Or, s∞ p²÷Fm

So, s= kp²÷Fm

From iii number equation- s= p÷2Fm

So, k=½

Conditions of this law: 

There are some conditions of this law. They are-

i) The object should be a moving object. 

ii) This formula applies to moving objects in a plane. This formula does not apply to tilted surfaces, freely falling objects and stationary objects.

Conclusion: 

So, if we know the value of object’s momentum, mass and applied force, we can determine the value of object’s displacement.